Mecânica Celeste: as 3 Leis de Kepler e a Gravitação Universal

As dicas do Tonho sobre Kepler:

1. Kepler estabeleceu de forma definitiva como os planetas se movem ao redor do sol.
2. Com a ajuda do astrônomo Tycho Brahe (1546-1601), que trabalhou com ele em seu observatório até sua morte, Kepler foi capaz de enunciar três leis que permanecem válidas até hoje.
3. O mais incrível de tudo é que Kepler e Tycho descobriram tudo isso muitos séculos antes dos computadores e dos modernos telescópios digitais.
4. Veja a videoaula novamente, para perceber como eles fizeram descobertas geniais, que mudaram a história da física e da astronomia.

Veja As Leis de Kepler

• 1ª Lei de Kepler :  As trajetórias dos planetas, em torno do Sol, têm forma elíptica, e o Sol ocupa um dos focos da elipse.
• 2ª Lei de Kepler :  O raio vetor que une o centro de massa do Sol e o centro da massa de um planeta varre áreas iguais em intervalos de tempo iguais.
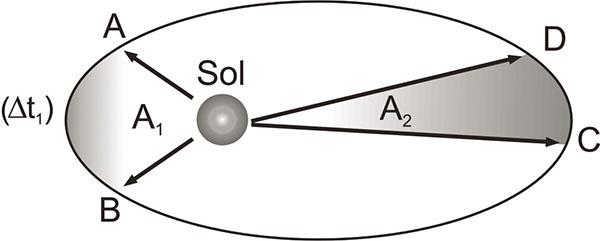
• t1 = t2   então  A1 = A2
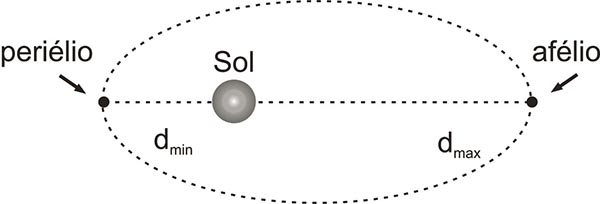
• Como consequência da 2ª Lei de Kepler, a velocidade de translação do planeta é variável, sendo máxima no periélio e mínima no afélio.
• O movimento de translação somente seria uniforme se a órbita fosse circular.
• Na imagem a seguir você consegue ‘ver’ o ponto em que a Terra está mais próxima do Sol, no Periélio, e o ponto mais distante, no Afélio.






3ª Lei de Kepler

Para todos os planetas de um sistema solar é constante a razão entre o cubo do raio médio da órbita (semieixo maior da elipse) e o quadrado do período.





O esquema da Lei da Gravitação Universal






• A força gravitacional entre dois pontos materiais tem intensidade diretamente proporcional ao produto de suas massas, e inversamente proporcional ao quadrado da distância que os separa.
• 
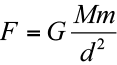
• G = constante de gravitação universal.
• 
  

Entenda os Satélite artificiais estacionários:

a. órbita contida no plano equatorial da Terra;
b. órbita circular para que o movimento seja uniforme;
c. período de translação igual ao período de rotação da Terra: 24 horas;
d. raio de órbita obtido aplicando-se a 3ª Lei de Kepler e comparando com a Lua.

Atividades-3ª Lei de Kepler

1-Em setembro de 2010, Júpiter atingiu a menor distância da Terra em muitos anos. As figuras abaixo ilustram a situação de maior afastamento e a de maior aproximação desses planetas, considerando que suas órbitas são circulares, que o raio da órbita terrestre (R_T) mede 1,5.10¹¹ m e que o raio da órbita de Júpiter (R_J) equivale a 7,5.10¹¹ m.



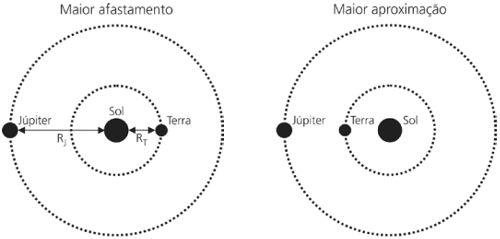
De acordo com a Terceira Tei de Kepler, o período de revolução e o raio da órbita desses planetas em torno do Sol obedecem à relação:



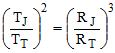
Em que T_J e T_T são os períodos de Júpiter e da Terra, respectivamente. Considerando as órbitas circulares representadas na figura acima, o valor de T_J, em anos terrestres, é mais próximo de:

a) 0,1

b) 5

c) 12

d) 125

2-Determine por meio da lei dos períodos proposta por Kepler o período de revolução de um planeta que está a 9 UA do Sol.

Dado: UA: unidade astronômica.

a) 30 anos

b) 25 anos

c) 17 anos

d) 27 anos

e) 12 anos

3-Quando o raio médio da órbita de um planeta está em unidade astronômica (UA), e o período de revolução está em anos terrestres, o resultado da lei dos períodos aplicada a qualquer planeta deve tender a 1. Qual deverá ser o raio médio da órbita de um planeta qualquer do sistema solar, em UA, que possui período de translação de oito anos?

a) 0,5  b) 1  c) 2  d) 3 e) 4

4-(UFPB) Recentemente, noticiou-se a chegada do robô Curiosity a Marte. Antes de descer sobre a superfície, o robô orbitou em torno de Marte com uma trajetória circular de raio R e período T. Esse mesmo satélite orbitaria em torno da Terra com um trajetória circular de raio 3R e período 2T. Sabendo que a Terceira Lei de Kepler é dada por:

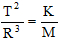
Em que M é a massa do corpo central, e K uma constante, identifique a razão entre as massas da Terra e de Marte:

a) 27/4

b) 3/2

c) 9/8

d) 8/9